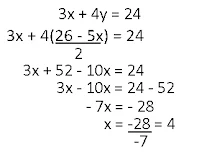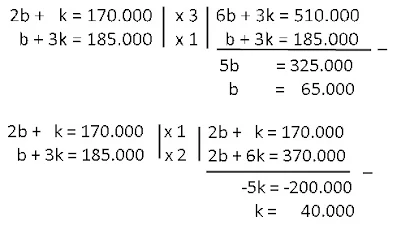Portalhot Bimbel Jakarta Timur, Bimbel Matematika, IPA, Fisika, Kimia, Biologi, Komputer, SD SMP SMA, Jakarta Timur, Hp: 082210027724
Sistem persamaan linear dua variabel by Bimbel jakarta Timur, yang di pelajari kelas 8 sering kita gunakan untuk materi lain baik dalam pelajaran matematika, juga pada pelajaran lain seperti fisika, ekonomi dan lainnya. Sistem persamaan linear dua variabel, tiga variabel digunakan untuk menentukan solusi suatu persamaan
Sistem persamaan linear adalah sekumpulanpersamaan linear (garis lurus) yang terdiri dari beberapa variabel yang dari sistem tersebutdapat ditentukan nilai dari variabel yang diberikan.Apa sih variabel itu? Variabel atau peubah adalahlambang pengganti suatu bilangan yang belum diketahui nilainya dengan pasti. Nahhhpada sistem persamaan ini kita dapat mengetahui nilai variabel yang diberikan.Bagaimana caranya? Ada beberapa cara yang bisa digunakan untuk mencari nilai ataupenyelesaian sistem persamaan linear dua variabel.
1. Metode grafik
Cara inidilakukan dengan menggambar masing-masing persamaan yang diberikan pada diagramkartesius hingga ditemukan sebuah titik potong. Titik potong yang didapat ituadalah penyelesaian sistem persamaan tersebut.
Contoh :
Tentukanhimpunan penyelesaian dari sistem persamaan linear berikut :
a. x + y=6 dan 2x + y=8
b. 3x + 2y=12 dan x + 2y=8
Jawab :
a. Untuk menggambar grafik persamaan linear, kita harus mencari titik potong garis terhadap sumbu x dan sumbu y. Titik potong garis terhadap sumbu x didapat jika nilai y=0, sebaliknya titik potong terhadap sumbu y didapat jika nilai x=0. Setelah didapatkan dua titik potong tersebut maka dapat ditarik garis yang melewati kedua titik.
Garis x + y=6
Titik potong sumbu x ( y=0)
x + 0=6
x=6
titik potong (6,0)
Titik potong sumbu y (x=0)
0 + y=6
y=6
titik potong (0,6)
Tarik garis yang melewati kedua titik maka didapatkan garis seperti yg tergambar dengan garis warna biru pada diagram kartesius di bawah.
Garis 2x + y=8
Titik potong sumbu x ( y=0)
2x + 0=8
2x=8
x=4
titik potong (4,0)
Titik potong sumbu y (x=0)
2(0) + y=8
y=8
titik potong (0,8)
Tarik garis yang melewati kedua titik maka didapatkan garis seperti yg tergambar dengan garis warna merah pada diagram kartesius di bawah.
 |
| SPLDV Metode Grafik |
Kedua garis yang telah digambar berpotongan pada titik (2,4). Maka penyelesaian dari sistem persamaan linear tersebut adalah (2,4) yang artinya nilai x=2 dan nilai y=4.
b. Garis 3x + 2y=12
Titik potong sumbu x ( y=0)
3x + 2(0)=12
3x=12
x=4
titik potong (4,0)
Titik potong sumbu y (x=0)
3(0) + 2y=12
2y=12
y=6
titik potong (0,6)
Pada gambar di bawah ditunjukkan dengan garis biru
Garis x + 2y=8
Titik potong sumbu x ( y=0)
x + 2(0)=8
x=8
titik potong (8,0)
Titik potong sumbu y (x=0)
0 + 2y=8
2y=8
y=4
titik potong (0,4)
Pada gambar dibawah ditunjukkan dengan garis merah
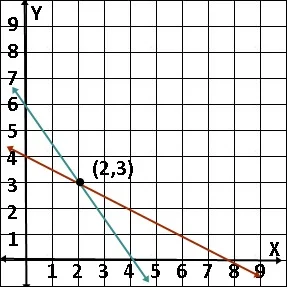 |
| SPLDV Metode Grafik |
Kedua garis yang telah digambar berpotongan pada titik (2,3). Maka penyelesaian dari sistem persamaan linear tersebut adalah (2,3) yang artinya nilai x=2 dan nilai y=3.
2. Metode Substitusi
Metode Substitusi adalah suatu metode mencari penyelesaian persamaan dengan cara mensubstitusi (mengganti) salah satu variabelnya dengan persamaan lain ataupun dengan nilai yang sudah diketahui.
contoh :
a. 3x + y=0 dan 2x – 3y=11
b. 4x + 3y=6 dan 2x – y=3
c. 3x+ 4y=24 dan 5x + 2y=26
Jawab :
a. Pilih salah satu persamaan yang akan kita substitusi ke persamaan lain. Lalu ubah salah satu variabelnya menjadi bentuk persamaan ekuivalen.
Kita pilih persamaan 3x + y=0
Ubah dengan memindahkan 3x ke ruas kanan sehingga bentuknya menjadi
y=- 3x
Substitusi nilai y ke persamaan yang lain
2x - 3y=11
2x - 3 (-3x)=11
2x + 9x=11
11x=11
x=1
Substitusi nilai x ke salah satu persamaan yang kita inginkan
2x - 3y=11
2(1) - 3y=11
2 - 3y=11
- 3y=11 - 2
- 3y=9
y=9/-3
y=-3
Penyelesaian (1,-3)
b. 4x + 3y=6 dan 2x – y=3
Misalkan dipilih 2x - y=3
2x - y=3
- y=3 - 2x
y=2x - 3
Substitusi ke persamaan 4x + 3y=6
4x + 3(2x - 3)=6
4x + 6x - 9=6
10x=6 + 9
10x=15
x=15/10=1½
Substitusi nilai x ke salah satu persamaan
2x - y=3
2(1½) - y=3
3 - y=3
- y=3 - 3
- y=0
y=0
Penyelesaian (1½, 0)
Substitusi nilai x ke salah satu persamaan
5x + 2y=26
5(4) + 2y=26
20 + 2y=26
2y=26 - 20
2y=6
y=6/3=2
Penyelesaiannya adalah (4,2)
Maka harga 1 baju adalah Rp 65.000,00 dan harga 1 kaos Rp 40.000,00.
Harga 3 baju dan 2 kaos adalah
3b + 2k=3(65.000) + 2 (40.000)
=195.000 + 80.000
=Rp 275.000,00
3. Keliling sebuah persegi panjang sama dengan 44 cm. Jika lebarnya 6 cm lebih pendek dari panjangnya, Tentukan luas dari persegi panjang tersebut.
Jawab :
Rumus keliling=2 (p + l)=2p + 2l, maka
2p + 2l=44
p - l=6 ⇒ p=6 + l
2p + 2l=44
2(6 + l) + 2l=44
12 + 2l + 2l=44
4l=44 -12
4l=32
l=8 cm
p=6 + l
p=6 + 8=14 cm
Luas=p x l
=14 cm x 8 cm
=112 cm²
Jumlah risol yang dijual adalah 16 buah dan bolu 24 buah.
Keuntungan yang diperoleh adalah
500a + 500b=400(16) + 500(24)
=6.400 + 12.000
=Rp 18.400,00
Demikian materi Sistem Persamaan Linear Dua Variabel dan berberapa contoh soal serta pembahasan yang diberikan Bimbel Diah Jakarta Timur. Semoga dapat membantu untuk lebih memahami.
5x + 2y=26
5(4) + 2y=26
20 + 2y=26
2y=26 - 20
2y=6
y=6/3=2
Penyelesaiannya adalah (4,2)
3. Metode Eliminasi
Metode Eliminasi adalah suatu metode mencari penyelesaian persamaan dengan cara mengeliminasi (menghilangkan) salah satu variabelnya. Menghilangkan variabel adalah dengan cara menyamakan koefisien variabel yang dipilih terlebih dahulu.
contoh :
a. 4x - 5y=-9 dan 2x + 3y=23
b. 4x - 3y=15 dan -3x + 2y=- 12
Jawab
a. Jika ingin mengeliminasi variabel x maka samakan koefisien variabel x menjadi KPK dari kedua koefisien.
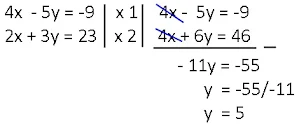 |
| penyelesaian |
Jika koefisien variabel yang dieliminasi bertanda sama (sama-sama negatif atau sama-sama negatif), maka eliminasi dengan cara mengurangi. Tetapi jika koefisien variabel yang ingin dieliminasi berbeda, maka eliminasi dengan cara menjumlah.
 |
| penyelesaian |
Penyelesaiannya adalah (4,5)
b. Eliminasi variabel x
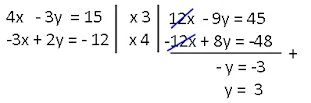 |
| penyelesaian |
Eliminasi variabel y
 |
| penyelesaian |
Penyelesaiannya adalah (6,3)
4. Metode Eliminasi dan Substitusi
Metode berikut menggunakan eliminasi untuk mendapatkan nilai dari salah satu variabel. Kemudian variabel yang sudah diketahui nilainya disubstitusi ke salah satu persamaan untuk mendapatkan nilai variabel yang lain.
contoh :
Tentukan himpunan penyelesaian sistem persamaan
2x +3y=12 dan 4x -7y=-2
Jawab :
Eliminasi variabel x
 |
| penyelesaian |
Substitusi nilai y ke persamaan 2x + 3y=12
2x + 3(2)=12
2x + 6 =12
2x =12 -6
2x =6
x =6/2=3
Himpunan penyelesaian{(3,2)}
Selain metode-metode penyelesaian di atas, ada beberapa model sistem persamaan linear yang membutuhkan penyelesaian tambahan. Perhatikan beberapa contoh sistem persamaan berikut, tentukan himpunan penyelesaiannya.
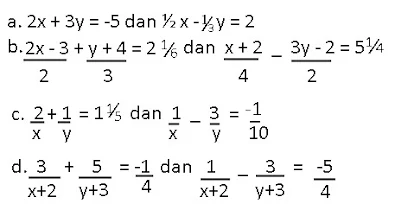 |
| penyelesaian |
Jawab
a. Persamaan kedua berupa pecahan, agar lebih mudah maka kedua ruas dikali dengan KPK penyebutnya agar koefisien variabel berupa bilangan bulat.
½x - ⅓ y=2......... dikali 6
3x - 2y=12
Lanjutkan penyelesaian dengan metode yg telah dibahas sebelumnya, misalnya metode eliminasi.
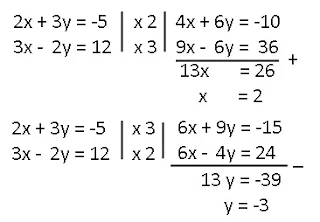 |
| penyelesaian |
Himpunan penyelesaian{(2, -3)}
b. Persamaan pertama dikali 6
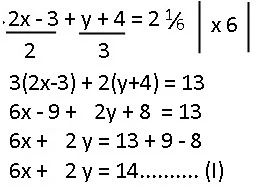 |
| penyelesaian |
Persamaan kedua dikali 4
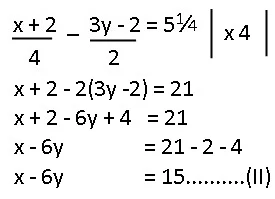 |
| penyelesaian |
Lanjutkan penyelesaian dari (I) dan (II)
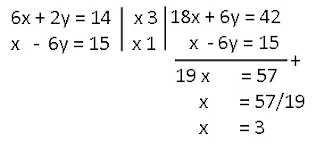 |
| penyelesaian |
x - 6y=15
3 - 6y=15
- 6y=15 -3
- 6y=12
y=12/-6
y=-2
Himpunan penyelesaian{(3,-2)}
c. Misalkan a=1/x dan b=1/y, maka
persamaan I menjadi 2a + b=6/5
persamaan II menjadi a - 3b=-1/10 → a=3b - 1/10
Substitusi ke 2a + b=6/5
2(3b - 1/10) + b=6/5
6b - 1/5 + b =6/5
6b + b =6/5 + 1/5
7b =7/5
b =1/5
1/y =1/5, maka y=5
a=3b - 1/10
a=3(1/5) - 1/10
a=3/5 - 1/10
a=5/10
a=1/2
1/x=1/2
x =2
Himpunan penyelesaian{(2,5)}
d. Misalkan a=1/(x+2), b=1/(y+3) maka
3a + 5b=-1/4
a - 3b=-5/4 → a=3b - 5/4
Substitusi ke 3a + 5b=-1/4
3(3b - 5/4) + 5b=-1/4
9b -15/4 + 5b =-1/4
9b + 5b =-1/4 + 15/4
14b =14/4
b =1/4
1/(y+3) =1/4
y+3 =4
y =4 - 3=1
a=3b - 5/4
a=3(1/4) - 5/4
a=3/4 - 5/4
a=-2/4
a=-1/2
1/(x+2)=-1/2
x + 2 =-2
x =-2 - 2
x =-4
Himpunan penyelesaian{(-4,1)}
Contoh soal cerita
1. Harga3 pensil dan 2 buku tulis adalah Rp5.100,00. Sedangkan harga 2 pensil dan 4buku tulis adalah Rp7.400,00. Model matematika yang tepat untuk pernyataantersebut adalah….
Jawab :
Misalkan hal yang diketahui menjadi variabel yang sesuai, misalnya x dan y, a dan b, p dan q dan sebagainya. Untuk menjawab soal ini kita misalkan pensil dengan p dan buku dengan b.
3 pensil dan 2 buku tulis adalah Rp5.100,00
⇒3p + 2b=5.100
2 pensil dan 4 buku tulis adalah Rp7.400,00
⇒ 2p + 4b=7.400
bisa disederhanakan dengan sama-sama dibagi 2
⇒ p + 2b=3.700
Jawab :
Misalkan hal yang diketahui menjadi variabel yang sesuai, misalnya x dan y, a dan b, p dan q dan sebagainya. Untuk menjawab soal ini kita misalkan pensil dengan p dan buku dengan b.
3 pensil dan 2 buku tulis adalah Rp5.100,00
⇒3p + 2b=5.100
2 pensil dan 4 buku tulis adalah Rp7.400,00
⇒ 2p + 4b=7.400
bisa disederhanakan dengan sama-sama dibagi 2
⇒ p + 2b=3.700
2. Jika harga2 buah baju dan 1 kaos adalah Rp.170.000,00. Sedangkan harga 1 baju dan 3 kaos adalahRp.185.000,00. Harga 3 baju dan 2 kaos adalah.....
Jawab :
Misalkan baju=b dan kaos=k
Sistem persamaan linear :
2b + k=170.000
b + 3k=185.000
Jawab :
Misalkan baju=b dan kaos=k
Sistem persamaan linear :
2b + k=170.000
b + 3k=185.000
Maka harga 1 baju adalah Rp 65.000,00 dan harga 1 kaos Rp 40.000,00.
Harga 3 baju dan 2 kaos adalah
3b + 2k=3(65.000) + 2 (40.000)
=195.000 + 80.000
=Rp 275.000,00
3. Keliling sebuah persegi panjang sama dengan 44 cm. Jika lebarnya 6 cm lebih pendek dari panjangnya, Tentukan luas dari persegi panjang tersebut.
Jawab :
Rumus keliling=2 (p + l)=2p + 2l, maka
2p + 2l=44
p - l=6 ⇒ p=6 + l
2p + 2l=44
2(6 + l) + 2l=44
12 + 2l + 2l=44
4l=44 -12
4l=32
l=8 cm
p=6 + l
p=6 + 8=14 cm
Luas=p x l
=14 cm x 8 cm
=112 cm²
4.Bibi menjual dua jenis kue yaitu risol dan bolu. Keranjang berdagangnya hanya dapatmemuat 40 buah kue. Harga modal risol adalah RP 1.500,00 perbuah, sedangkanharga modal bolu adalah Rp 2.000,00. Modal yang ia keluarkan adalah Rp72.000,00. Berapa pendapatan Bibi jika penjualan risol untungnya Rp 400,00 perbuah dan bolu memberikan untung Rp 500,00 perbuah?
Jawab :
Misalkan risol=a dan bolu=b
jumlah kue=40 ⇒ a + b=40
modal kue ⇒ 1.500a + 2.000b=72.000 (sederhanakan dengan dibagi 500)
⇒ 3a + 4b=144
Jawab :
Misalkan risol=a dan bolu=b
jumlah kue=40 ⇒ a + b=40
modal kue ⇒ 1.500a + 2.000b=72.000 (sederhanakan dengan dibagi 500)
⇒ 3a + 4b=144
Keuntungan yang diperoleh adalah
500a + 500b=400(16) + 500(24)
=6.400 + 12.000
=Rp 18.400,00
Demikian materi Sistem Persamaan Linear Dua Variabel dan berberapa contoh soal serta pembahasan yang diberikan Bimbel Diah Jakarta Timur. Semoga dapat membantu untuk lebih memahami.