Articles by "Metode"

Showing posts with label Metode. Show all posts

GRADIEN DAN PERSAMAAN GARIS LURUS By Bimbel Jakarta Timur

Radarhot.com - September 05, 2024 0

Portalhot Bimbel Jakarta Timur, Bimbel Matematika, IPA, Fisika, Kimia, Biologi, Komputer, SD SMP SMA, Jakarta Timur, Hp: 082210027724

Gradien adalah kemiringan suatu garis.

sedangkan Garis Lurus adalah garis yang menghubungkan dua titik. Persamaan garis lurus menunjukkan perbandingan komponen y dan komponen x yang dilalui titik yang dimaksud.

Menentukan gradien garis berdasarkan gambar

Gradien garis dapat dihitung dengan :
komponen perpindahan vertikal (y)
komponen perpindahan horisontal (x)

Komponen y ke atas bernilai positif, sedangkan jika ke arah bawah bernilai negatif.
Komponen x ke kanan bernilai positif, sedangkan jika ke kiri bernilai negatif.

Perhatikan gambar berikut !

Bimbel Jakarta Timur CPNS Geometri Matematika Metode

Bangun Ruang Sisi Datar by Bimbel Jakarta Timur

Radarhot.com - September 05, 2024 0

Portalhot Bimbel Jakarta Timur, Bimbel Matematika, IPA, Fisika, Kimia, Biologi, Komputer, SD SMP SMA, Jakarta Timur, Hp: 082210027724

Bangun Ruang Sisi Datar by Bimbel Jakarta Timur

| Bangun Ruang Sisi Datar adalah bangun tiga dimensi yang pada setiap rusuknya berbentuk garis dan tidak melengkung. Bangun ruang memiliki luas permukaan dan volume atau isi.

KUBUS

Kubus adalah bangun ruang sisi datar yang berbentuk prisma segiempat yang memiliki rusuk sama panjang. Kubus terdiri dari 6 persegi yang sama besar.

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990

kubus

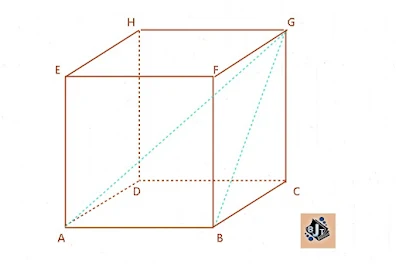
Pada gambar kubus ABCD.EFGH di atas disimpulkan bahwa kubus memiliki :

12 rusuk yaitu AB, BC, CD, AD, EF, FG, GH, EH, AE, BF, CG, DH
6 bidang berbentuk persegi yaitu ABCD, EFGH, ABFE, CDHG, ADHE, BCGF
12 diagonal bidang yaitu AC, BD. EG, FH, AF, BE, DG, CH, BG, CF, AH, DE
12 bidang diagonal yaitu ABGH, CDEF, BCHE, ADGFACGE, BDHF
4 diagonal ruang yaitu AG, BH,CE, DF

Jika rusuk kubus adalah s, maka

Rumus Kubus BJT

BALOK

Balok adalah bangun ruang yang terdiri dari 3 pasang segiempat.

Balok

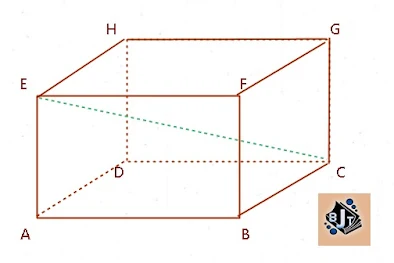
Dari gambar di atas, kita dapat simpulkan bahwa balok memiliki :

12 rusuk yaitu 4 rusuk panjang AB, CD, EF, GH, 4 rusuk lebar yaitu AD, BC, FG, EH dan 4 rusuk tinggi AE, BF, CG, DH
6 bidang yaitu ABCD, EFGH, ABFE, CDHG, ADHE, BCGF
12 diagonal bidang yaitu AC, BD. EG, FH, AF, BE, DG, CH, BG, CF, AH, DE
12 bidang diagonal yaitu ABGH, CDEF, BCHE, ADGFACGE, BDHF
4 diagonal ruang yaitu AG, BH,CE, DF

Rumus Balok BJT

Prisma

Prisma adalah bangun ruang yang sisi alas dan tutupnya merupakan bangun datar dengan bentuk dan ukuran yang sama serta sisi tegak prisma merupakan segi empat. Prisma bisa berbentuk prisma segitiga, prisma segiempat, prisma segi-lima dan lain-lain. Kubus dan balok merupakan contoh prisma segi-empat.

Prisma

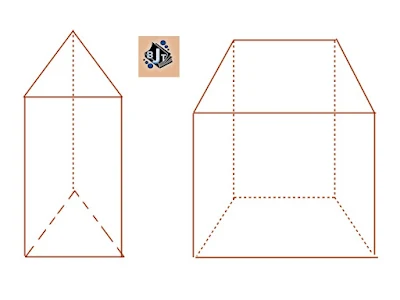
Dari gambar di atas, kita dapat simpulkan bahwa prisma memiliki :

jumlah rusuk prisma segi-n adalah 3 x n
jumlah bidang prisma segi-n adalah n + 2
jumlah sudut prisma segi-n adalah 2 x n

Rumus Prisma BJT

Limas

Limas adalah bangun ruang yang memiliki sisi alas dengan sisi tegak berbentuk segitiga. Limas bisa berbentuk limas segitiga, limas segiempat, limas segi-lima dan lain-lain. Bidang empat adalah sebutan untuk limas segitiga yang semua panjang rusuknya sama besar.

Limas

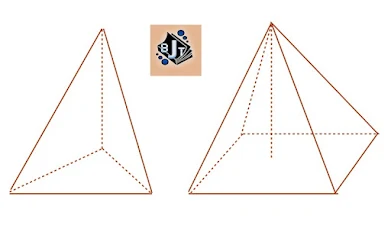
Dari gambar di atas, kita dapat simpulkan bahwa limas memiliki :

jumlah rusuk limas segi-n adalah 2 x n
jumlah bidang prisma segi-n adalah n + 1
jumlah sudut prisma segi-n adalah n + 1

Rumus Limas BJT

Contoh soal

1. Diketahui panjang DF pada kubus di bawah iniadalah 6√3cm.

soal nomor 1

Tentukanlah:

a. Panjang rusuk kubus
b. Luas permukaan kubus
c. Volume kubus

Jawab :

a. DF adalah diagonal ruang,

sehingga s √3=6√3

s=6 cm

b. Luas permukaan kubus

= 6 x s²

= 6 x 6²

=6 x 36

=216 cm²

c. Volume kubus

=s³

=6³

=216 cm³

2. Sebuah kubus berukuran 12 cm x 4 cm x 3 cm.

Tentukanlah :

a. Panjang diagonal ruang balok
b. Luas permukaan balok
c. Volume balok

Jawab :

a. Panjang diagonal ruang balok

=√(p² + l² + t² )

=√(12² + 4² + 3²)

=√(144 + 16 + 9)

=√169

=13 cm

b. Luas permukaan balok

=(2 x p x l) + ( 2 x p x t) + (2 x l x t)

=(2 x 12 x 4) + (2 x 12 x 3) + (2 x 4 x 3)

=96 + 72 + 24

=192 cm²

c. Volume balok

=p x l x t

=12 x 4 x 3

=144 cm³

3. Sebuah kubus mempunyai volume 512 cm³.

Tentukanlah :

a. Panjang rusuk kubus

b. Luas permukaan kubus

Jawab :

a. volume kubus=s³,

maka rusuk kubus,

s=∛V

s=∛512=8 cm

b. Luas permukaan kubus

=6 x s²

=6 x 8²

=384 cm²

4. Diketahui sebuah balok mempunyai luas sisi alas 120 cm², luas sisi depan 75 cm² dan luas sisi samping 40 cm². Tentukanlah volume balok serta ukuran panjang, lebar dan tinggi balok !

Jawab :

Luas sisi alas x luas sisi depan x luas sisi samping=(p x l) x (p x t) x (l x t)=p² x l² x t²=(p x l x t)²

maka Volume=√(p x l) x (p x t) x (l x t)

=√(120 x 75 x 40)

=√360.000

=600 cm³

panjang=√(p x l) x (p x t) : (l x t)

=√(120 x 75 : 40)

=√225

=15 cm

lebar= √(p x l) x (l x t) : (p x t)

=√(120 x 40 : 75)

=√64

=8 cm

tinggi= √(p x t) x (l x t) : (p x l)

=√(75 x 40 : 120)

=√25

=5 cm

5. Sebuah prisma memiliki alas segitiga siku-siku dengan ukuran sisi 5cm, 12 cm dan 13 cm dan tinggi prisma 20 cm. Tentukan luas permukaan dan volume prisma tersebut !

Jawab :

Luas permukaan

=(2 x luas alas) + ( keliling alas x tinggi prisma)

=( 2 x 5 x 12 : 2) + (5 + 12 + 13) x 20

=60 + 600

=660 cm²

Volume

= luas alas x tinggi prisma

=(5 x 12 :2 ) x 20

=600 cm³

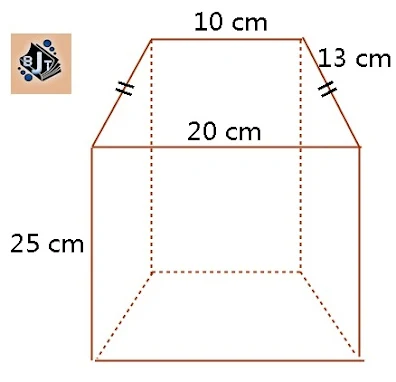
6. Diketahui prisma trapesium seperti gambar di bawah.

Tentukan luas permukaan dan volume prisma tersebut !

soal nomor 6

Jawab :

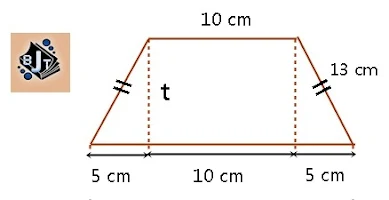
Perhatikan gambar trapesium berikut !

jawaban soal nomor 6

Terlebih dahulu kita tentukan tinggi trapesium dengan menggunakan dalil phytagoras.

5² + t²=13²

25 + t²=169

t²=169 - 25=144

t=√144=12 cm

Luas permukaan prisma

=(2 x luas alas) + ( keliling alas x tinggi prisma)

=(2 x (10 + 20) x 12 : 2) + (13 + 10 + 13 + 20) x 25

=360 + 1.400

=1.760 cm²

Volume prisma

=luas alas x tinggi prisma

=((10 + 20) x 12 : 2) x 25

=180 x 25

=4.500 cm³

7. Sebuah limas alasnya berbentuk persegi dengan panjang rusuk alas 16 cm dan tinggi limas 15 cm.

Tentukanlah :

a. Luas permukaan limas

b. Volume limas

Jawab :

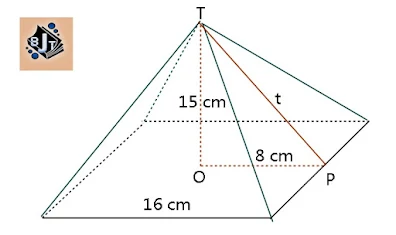
a. Perhatikan gambar limas persegi berikut !

Limas persegi

Terlebih dahulu kita mencari tinggi bidang tegak segitiga yang pada gambar ditunjukkan oleh garis TP. Garis OP panjangnya adalah 1/2 dari panjang rusuk yaitu 1/2 x 16=8 cm.

Dari segitiga TOP kita cari panjang TP dengan dalil phytagoras.

TP²=TO² + OP²

=15² + 8²

=225 + 64

=289

TP =√289=17 cm

Maka luas permukaan

=Luas alas + 4 x luas segitiga

=(16 x 16) + 4 x (16 x 17 : 2)

=256 + 544

=800 cm²

b. Volume limas

=1/3 x luas alas x tinggi limas

=1/3 x 256 x 15

=1.280 cm³

8. Andi memiliki sebuah kotak berbentuk balok untuk menyimpan mainannya. Kotak tersebut berukuran 90 cm x 75 cm x 30 cm. Kotak mainan tersebut diisi mainan kardus-kardus mainan berbentuk kubus dengan panjang rusuk 15 cm. Berapa banyak kardus kubus yang dapat mengisi kotak mainan tersebut?

Jawab :

Jumlah kubus yang dapat mengisi kotak balok

=Volume balok : volume kubus

=(90 x 75 x 30 ) : (15 x 15 x 15)

=60 buah

9. Sebuah akuarium berbentuk balok berukuran panjang 1,2 m, lebar 75 cm dan tinggi 60 cm. Jika akuarium tersebut diisi air sampai 2/3 tingginya, berapa liter volume air dalam akuarium tersebut?

Jawab :

Karena liter=dm³, maka semua ukuran dirubah ke dalam satuan dm

p=1,2 m=12 dm

l =75 cm=7,5 dm

t=60 cm=6 dm

Volume air

=2/3 x volume akuarium

=2/3 x 12 x 7,5 x 6

=360 dm³

=360 liter

10. Farlan hendak membuat tenda dari kain terpal yang berbentuk limas persegi panjang. Tenda itu ukuran alasnya 3,2 m x 1,8 m dan tinggi 1,2 m. Jika tenda yang dibuat Farlan tidak menggunakan alas, maka tentukan luas kain terpal yang dibutuhkan !

Jawab :

Perhatikan gambar di bawah !

Limas Persegi Panjang

Segitiga di bagian depan berukuran sama dengan segitiga bagian belakang yaitu panjang alasnya 3,2 m dan tingginya adalah ruas TQ. Panjang TQ bisa dihitung dengan dalil phytagoras dari segitiga TQO.

TQ²=TO² + QO²

=1,2² + 0,9²

=1,44 + 0,81

=2,25

TQ=√2,25=1,5 m

Segitiga di bagian kiri berukuran sama dengan segitiga bagian kanan yaitu panjang alasnya 1,8 m dan tingginya adalah ruas TP. Panjang Tp bisa dihitung dengan dalil phytagoras dari segitiga TPO.

TP²=TO² + PO²

=1,2² + 1,6²

=1,44 + 2,56

=4,00

TP=√4,00=2,0 m

Maka luas kain terpal yang dibutuhkan

=2 x luas segitiga depan + 2 x segitiga samping

=2 x (3,2 x 1,5 : 2) + 2 x (1,8 x 2,0: 2)

=4,8 + 3,6

=8,4 m²

Demikian rangkuman materi tentang bangun ruang sisi datar beserta contoh soal dan pembahasannya. Semoga dapat membantu anda untuk lebih memahami materi tersebut.

https://www.radarhot.com/2018/10/bangun-ruang-sisi-datar.html

Bimbel Jakarta Timur IPA Kimia Metode Soal

STOIKIOMETRI by Bimbel Jakarta Timur

Radarhot.com - September 03, 2024 0

Portalhot Bimbel Jakarta Timur, Bimbel Matematika, IPA, Fisika, Kimia, Biologi, Komputer, SD SMP SMA, Jakarta Timur, Hp: 082210027724

Dalam Artikel ini Bimbel Jakarta Timur akan membahas secara Khusus mengenai Stoikiometri yaitu cabang ilmu kimia yang mempelajari dan menghitung hubungan kuantitatif antara pereaksi (reaktan) dan hasil reaksi (produk) dalam persamaan kimia.

Hukum-hukum Dasar Kimia

1. Hukum kekekalan massa (hukum Lavoisier) : massa total zat-zat sebelum reaksi akan selalu sama dengan massa total zat-zat setelah reaksi.

contoh : 3 gram gas hidrogen(H₂) yang bereaksi dengan 24 gram gas oksigen (O₂) akan membentuk 27 gram air (H₂O)

Hukum kekekalan massa

2. Hukum perbandingan tetap (hukum Proust) : perbandingan massa unsur dalam senyawa selalu tetap.

contoh :

H₂	O₂	H₂O	Keterangan
1 gram	8 gram	9 gram
2 gram	8 gram	9 gram	sisa H₂=1 gram
2 gram	17 gram	18 gram	sisa O₂=1 gram
4 gram	25 gram	27 gram	sisa H₂=1 gram, O₂=1 gram

3. Hukum perbandingan berganda ( hukum Dalton) : jika dua unsur dapat membentuk lebih dari satu senyawa dan massa salah satu unsur tersebut tetap(sama), perbandingan massa unsur yang lain dalam senyawa tersebut merupakan bilangan bulat sederhana.

contoh :

Perbandingan H : O dalam H₂O =2 : 16=1 : 8

Perbandingan H : O dalam H₂O₂=2 : 32=1 : 16

Dalam hidrogen yang sama massanya dapat bersenyawa dengan oksigen yang massanya berbanding sebagai 8 :16 atau 1 : 2

4. Hukum perbandingan volume (hukum Gay –Lussac) : volume gas-gas yang bereaksi dan gas-gas hasil reaksi jika diukur pada suhu dan tekanan yang sama berbanding sebagai bilangan bulat dan sederhana.

contoh :

Gas pentana C₅H₁₂ yang mempunyai volume 2 liter dibakar sempurna menurut reaksi :

C₅H₁₂+ 8 O₂ ⇒ 5 CO₂ + 6 H₂O

Tentukan volume gas oksigenyang dibutuhkan dan volume gas karbondioksida serta uap air yang terbentuk!

Jawab :

Perbandingan koefisien C₅H₁₂ : O₂ :CO₂ : H₂O=1 : 8: 5 : 6, maka

Volume O₂ yangdibutuhkan=8/1 x 2 liter=16 liter

Volume CO₂ yang terbentuk=5/1 x 2 liter=10 liter

Volume H₂O yang terbentuk=6/1 x 2 liter=12 liter

5. Hipotesis Avogadro : pada suhu dan tekanan yang sama, semua gas yang memiliki volume sama akan mengandung jumlah molekul yang sama.

contoh:

Jika diketahui uap air bervolume 250 ml, tentukanlah jumlah mol uap air tersebut pada keadaan dimana gas karbon dioksida bermassa 2,2 gram mempunyai volume 500 ml.

Jawab :

6. HukumBoyle – Gay Lussac : hasil kali tekanan gas dan volume gas akan selalu tetap jika dibagi suhu mutlak.

Rumus:

Massa Atom Relatif dan Massa MolekulRelatif

1. Massa atom dapat ditentukan dengan alat spectrometer massa. Hasil pembacaan spectrometer massa disebut spektrografmassa.

2. Satu satuanmassa atom (1 sma) : massa suatu partikel yang nilainya sebesar 1,67 x 10^-7kg.

3. Massa satu atom C-12 adalah 12 sma.

4. Massa atom relatif (Ar) adalah massa rata-ratasuatu atom relative (dibandingkan) dengan 1/12 kali massa atom C-12.

rumus 1

5. Massa atom relatif dari isotop-isotop di alam. Di alam, suatu unsur bisa didapatkan dalam dua jenis atau bahkan lebih isotop. Rumus menentukan atom relatifnya adalah :

rumus 2

6. Massa molekul relatif (Mr) merupakan jumlah massa atom relatif dari seluruh atom penyusun suatu molekul.

Persamaan Reaksi

1. Persamaan reaksi : cara memberikan lambang bagi suatu perubahan kimia (reaksi kimia). Persamaan reaksi menggambarkan rumus kimia zat-zat pereaksi dan zat-zat hasil reaksi.

2. Zat Perekasi (reaktan) :zat-zat yang mengalami perubahan dalam reaksi kimia.

3. Zat hasil reaksi (produk) :zat-zat hasil perubahan dalam reaksi kimia.

Perhitungan Kimia

Jembatan mol

1. Satu mol suatu zat : sejumlah partikel yang terkandung dalam suatu zat yang jumlahnya sama dengan 6,02 x 10²³partikel.

2. Tetapan Avogadro (L) : bilangan yang digunakan untuk menyatakan jumlah partikel satu mol zat yaitu 6,02 x 10²³partikel.

3. Massa molar : massa yang dimiliki oleh 1mol zat yang sama dengan massa atom relative atau massa rumus relatif zat tersebut dan dinyatakan dalam gram per mol.

4. Volume molar gas menyatakan volume yang ditempati satu mol gas pada suhu dan tekanan tertentu. Volume molar gas tidak tergantung pada jenisnya, tetapi pada jumlah mol, suhu dan tekanan pengukuran.

5. Standard Temperature Pressure (STP) : keadaan gas pada suhu 0^oC dan tekanan 1 atmosfer. Pada STP, volume molar gas sama dengan 22,4 L/mol.

6. Room Temperature Pressure (RTP) : keadaangas pada suhu 25^oC dan tekanan 1 atmosfer. Pada RTP, volume molar gas sama dengan 24,4 L/mol.

7. Kemolaran zat menyatakan jumlah mol zat terlarut dalam tiap liter larutan.

8. Pereaksi pembatas : pereaksi yang habis bereaksi terlebih dahulu dalam suatu reaksi kimia.

9. Rumus empiris : perbandingan paling sederhana dalam komposisi suatu senyawa.

Rumus molekul adalah kelipatan dari rumus empiris.

10. Hidrat : zat padat yang mengikat beberapamolekul air sebagai bagian dari struktur kristalnya.

contoh : CuSO₄.5H₂O,FeSO₄.7H₂O dan lain sebagainya.

Langkah-langkah Penyelesaian Perhitungan Kimia

1. Menuliskan persamaan reaksi lengkap dengan koefisien yang tepat.

2. Menghitung mol zat dari data yang diketahui dengan rumus yang sesuai.

3. Menentukan pereaksi pembatas berdasarkan perbandingan koefisien reaksi

4. Menentukan mol zat yang ditanyakan berdasarkan pada perbandingan koefisien reaksi.

5. Jawab pertanyaan dengan menggunakan molzat yang telah dicari pada tahap di atas.

contoh :

Sejumlah 3,2 gramgas metana (CH₄) dibakar dengan 16 gram gas oksigen. Berapa massa gas karbon dioksida yang terbentuk?

jawab :

1. Persamaan reaksi

CH₄ + 2 O₂ ⇒ CO₂ + 2 H₂O

2. Mol zat yang diketahui

nCH₄=massa/Mr =3,2/(12+4) =0,2 mol

nO₂= massa/Mr = 16/(2.16) =0,5 mol

3. Perbandingan koefisien dari persamaan reaksi (no.1)

CH₄: O₂ : CO₂ : H₂O=1 : 2 : 1 : 2

CH₄=0,2 mol/1 =0,2 mol

O₂= 0,5 mol/2=0,25 mol

hasil pembagian CH₄ lebih kecil dari O₂ , maka CH₄adalah pereaksi pembatas

4. Mol zat yang ditanyakan

nCO₂=1/1 x 0,2 mol=0,2 mol

5. Jawab pertanyaan

massaCO₂=n x Mr

=0,2 mol x (12+2(16))

=0,2 x 44

=8,8 gram

Pages

Instituteistic Math Science

GRADIEN DAN PERSAMAAN GARIS LURUS By Bimbel Jakarta Timur

Menentukan gradien garis berdasarkan gambar

Bangun Ruang Sisi Datar by Bimbel Jakarta Timur

KUBUS

BALOK

Prisma

Limas

Contoh soal

https://www.radarhot.com/2018/10/bangun-ruang-sisi-datar.html

STOIKIOMETRI by Bimbel Jakarta Timur

Hukum-hukum Dasar Kimia

Hukum kekekalan massa

Massa Atom Relatif dan Massa MolekulRelatif

Persamaan Reaksi

Langkah-langkah Penyelesaian Perhitungan Kimia

https://www.radarhot.com/2018/05/stoikiometri-hukum-hukum-dasar-kimia-1.html

Recent

Popular

Comments

Category