Articles by "video"
Showing posts with label video. Show all posts

- 0
Portalhot Bimbel Jakarta Timur, Bimbel Matematika, IPA, Fisika, Kimia, Biologi, Komputer, SD SMP SMA, Jakarta Timur, Hp: 082210027724
SOAL LATIHAN PAT MATEMATIKA KELAS 7 By Bimbel Jakarta Timur



Bimbel Jakarta Timur akan membagikan SOAL LATIHAN PAT MATEMATIKA KELAS 7 Ulangan Kenaikan Kelas (UKK) atau sekarang disebut Penilaian Akhir Tahun (PAT) adalah ujian yang sangat penting karena menentukan apakah siswa dapat melanjutkan ke kelas berikutnya. Untuk itu, siswa diharapkan dapat mempersiapkannya dengan optimal. Kami akan memberikan latihan soal UKK matematika kelas 7 untuk membantu siswa mempersiapkannya. Adapun materi yang termasuk dalam latihan ini adalah Aritmatika Sosial, Perbandingan, Garis dan Sudut, Segitiga dan Segiempat serta Penyajian Data. 


1. Seorang pedagang membeli 5 lusin pulpen dengan harga Rp 240.000,00. Jika ia menginginkan untung 15%, maka harga jual pulpen setiap batang adalah...

   A. Rp 4.150,00                        C. Rp 4.600,00
   B. Rp 4.300,00                        D. Rp 4.750,00

2. Sebuah toko memberikan diskon 12,5% untuk produk pakaian. Fira membeli 2 baju yang harganya masing-masing Rp 80.000,00 dan sebuah celana yang harganya Rp 60.000,00. Berapa uang yang harus dibayar Fira?

   A. Rp 187.500,00                     C. Rp 195.000,00
   B. Rp 192.500,00                     D. Rp 197.500,00

3. Seorang pedagang membeli sekarung kacang hijau yang memiliki bruto 50 kg dan tara 2%. Kacang hijau itu ia beli dengan harga Rp 600.000,00. Kacang hijau ia jual dengan harga Rp 13.000,00/kg sedangkan karungnya bisa dijual dengan harga Rp3.000,00. Berapa keuntungan yang diperoleh pedagang tersebut?

    A. Rp 37.000,00                     C. Rp 45.000,00
    B. Rp 40.000,00                     D. Rp 47.500,00

4. Fajar menabung Rp 5.000.000,00 di sebuah bank. Setelah 18 bulan, ia mengambil tabungannya yang ternyata telah berjumlah Rp 5.600.000,00. Berapakah suku bunga yang diberikan bank tersebut?

    A. 7,5%                                C. 9%
    B. 8 %                                  D. 12%

5. Pak Dono membeli sebuah lemari es dengan harga Rp 2.000.000,00. Karena membutuhkan uang, Pak Dono menjual lemari es tersebut dan mengalami kerugian 15%. Berapakah harga jual lemari es tersebut?

    A. Rp 1.850.000,00                  C.Rp 1.700.000,00 
    B. Rp 1.800.000,00                  D.Rp 1.500.000,00 

6. Ibu membutuhkan 15 meter kain untuk membuat 6 potong kain. Sebuah konveksi membuat baju yang modelnya sama sebanyak 2 lusin. Berapa banyak kain yang dibutuhkan konveksi tersebut?

     A. 80 meter                           C. 60 meter
     B. 72 meter                           D. 50 meter

7. Bu Ani membeli 5 liter beras dan membayar Rp 60.000,00. Bu Rini membeli 8 liter beras dari pedagang yang sama, berapa harga yang harus dibayar Bu Rini?

     A. Rp 108.000,00                    C. Rp 98.000,00
     B. Rp 102.000,00                    D. Rp 96.000,00

8. Kota a dan kota B yang jaraknya 30 km akan digambar pada sebuah peta dengan skala 1 : 2.000.000. Berapa jarak kota A dan kota B pada peta yang digambar?

      A. 1,5 cm                             C. 15 cm
      B. 2,5 cm                             D. 25 cm

9. Pak Rofik dan Pak Maman membeli pakan ternak dengan jumlah yang sama. Ternak Pak Rofik berjumlah 48 ekor dan pakan yang dibelinya akan habis dalam waktu 25 hari. Pak Maman membeli pakan tersebut untuk persediaan 30 hari. Berapa jumlah ternak yang dimiliki Pak Maman?

       A. 25 ekor                           C. 35 ekor
       B. 30 ekor                           D. 40 ekor

10. Ferdi berangkat ke kota P dengan motor berkecepatan rata-rata 45 km/jam. Ferdi sampai ditujuan dalam waktu 1 jam 40 menit. Pada perjalanan pulang menempuh rute yang sama, Ferdi memacu motornya dengan kecepatan 60 km/jam. Berapa waktu yang dibutuhkan Ferdi untuk sampai di rumah?

      A. 1 jam 30 menit                C. 1 jam 15 menit
      b. 1 jam 25 menit                D. 1 jam 10 menit

11. Sebuah proyek direncanakan dapat selesai dalam waktu 40 hari jika dikerjakan oleh 18 pekerja. Setelah berjalan 22 hari, pekerjaan terhenti selama 6 hari. Jika pekerjaan harus selesai sesuai jadwal, berapa pekerja tambahan yang diperlukan?

      A.  6 orang                          C. 18 orang
      B.  9 orang                          D. 27 orang

12. Perhatikan gambar berikut !

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
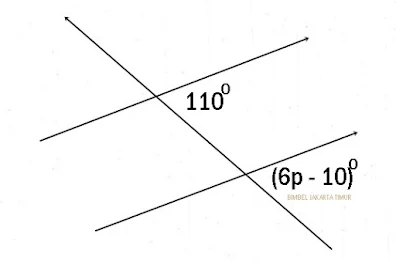Soal Nomor 12

Berapa besar p?

A. 20
B. 24
C. 30
D. 32


13. Perhatikan gambar di bawah ! 


Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
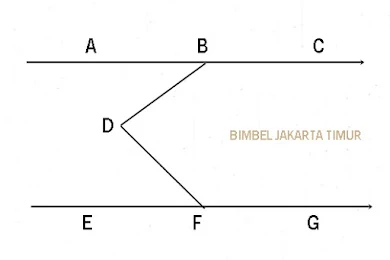Soal Nomor 13

Jika besar <ABD=32° dan <EFD=40°, maka besar <BDF=.... °

A. 64
B. 72
C. 80
D. 108


14. Besar <RQS pada gambar di bawah adalah... °

      
Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Soal Nomor 14

A. 20
B. 30
C. 40
D. 48




15. Besar < UQR pada gambar di bawah adalah ... °

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Soal Nomor 15

A. 72
B. 60
C. 54
D. 36



16. Tentukan nilai x pada gambar di bawah !

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
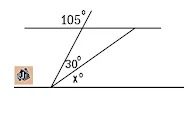Soal Nomor 16

A. 75
B. 65
C. 55
D. 45


17. Nilai x pada gambar di bawah adalah...

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Soal Nomor 17

A. 12
B. 15
C. 18
D. 20



18. Suatu segitiga samakaki memiliki panjang sisi yang sama 25 cm dan panjang sisi yang lain adalah 14 cm. Maka luas segitiga tersebut adalah.... cm²

     A. 64                                     C. 168
     B. 84                                     D. 180



19. Trapesium KLMN  dimana <K dan <N adalah siku-siku dengan panjang KL=27 cm, MN=15 cm dan KN=16 cm. Berapa keliling trapesium KLMN tersebut?

     A. 78 cm                                 C. 96 cm
     B. 84 cm                                 D. 102 cm

20. Luas sebuah persegi panjang adalah tiga kali luas persegi yang panjang sisinya 16 cm. Jika panjang persegipanjang tersebut adalah 32 cm, berapakah lebarnya?

      A. 18 cm                                 C. 26 cm
      B. 24 cm                                 D. 32 cm

21. Belah ketupat ABCD mempunyai keliling 52 cm. Jika panjang diagonal AC=10 cm, berapa luas bangun tersebut?

      A. 120 cm²                                 C. 240 cm²
      B. 130 cm²                                 D. 260 cm²

22. Sebuah jajargenjang PQRS besar <P=(5x-1)° dan <S=(2x+6)°. 
Tentukan besar <Q !

      A. 56°                                        C. 112°
      B. 62°                                        D. 124°

23. Tentukan luas daerah yang diarsir pada gambar berikut !

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Soal Nomor 23

A. 52 cm²
B. 48 cm²
C. 26 cm²
D. 24 cm²
 

24. Hitunglah jumlah segitiga yang terdapat pada gambar di bawah !

A. 20 buah
B. 32 buah
C. 48 buah
D. 55 buah



25. Sebuah kolam renang berbentuk persegipanjang berukuran 12 m x 8 m. Di sekeliling kolam dibuat jalan yang lebarnya 1m. Berapa luas jalan yang mengelilingi kolam tersebut?

  A. 36 m2                                       C. 56 m2
  B.44 m2                                       D. 64 m2

26. Diagram di bawah ini menunjukkan data hasil panen jeruk dalam waktu enam bulan.

Penurunan hasil panen terjadi dari bulan Februari ke Maret besarnya…. ton

Soal Nomor 26

A. 0,5                      
B. 1                          
       C. 1,5
       D. 2


27. Pada diagram nomer 26, kenaikan hasil panen tertinggi terjadi dari bulan…

A.      Januari ke Februari
B.     Februari ke Maret
C.      Maret ke April
D.     April ke Mei


28.Cara yang paling tepat untuk mengumpulkan data tentang tinggi badan siswa, adalah...

  A. observasi                                  C. angket
      B. kuisoner                                    D. dokumen

29. Pada diagram lingkaran di bawah adalah data cara siswa datang ke sekolah. Jika jumlah siswa yang dihitung dalam data tersebut adalah 200 orang, maka banyaknya siswa yang diantar menggunakan mobil ada….orang

Soal Nomor 29

A. 15                     B.  20                     C. 25                 D. 45 


30.Data rata-rata hasil ulangan semester I sebagai berikut :



Mata Pelajaran
Nilai rata-rata
PKn
85
IPA
70
IPS
75
B. Indonesia
80
Matematika
65
     

     Diagram batang dari data tersebut adalah…. 

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Soal Nomor 30

https://www.radarhot.com/2018/05/latihan-ukkpat-matematika-kelas-7.html



Continue reading

- 0
Portalhot Bimbel Jakarta Timur, Bimbel Matematika, IPA, Fisika, Kimia, Biologi, Komputer, SD SMP SMA, Jakarta Timur, Hp: 082210027724

Sebelum ke Rumus-Rumus, Contoh Soal dan Pembahasan Bimbel Jakarta Timur menjabarkan definisi secara Matematika, Fisika, Ekonomi dan Rekayasa


Dalam matematika

Turunan fungsi adalah konsep yang terkait dengan perubahan suatu fungsi terhadap variabel independennya. Dalam istilah yang lebih sederhana, turunan memberikan informasi tentang sejauh mana suatu fungsi berubah ketika nilai variabel independennya berubah. Turunan sering digunakan untuk mengukur kecepatan perubahan suatu fungsi pada suatu titik tertentu.

Interpretasi geometris dari turunan adalah sebagai gradien atau kemiringan garis singgung pada kurva fungsi pada titik tertentu. Turunan memberikan informasi tentang kecepatan perubahan nilai fungsi terhadap perubahan nilai variabel independennya.

Beberapa aturan turunan yang umum digunakan melibatkan aturan pangkat, aturan rantai, dan aturan jumlah/diferensiasi.

Dalam fisika

Turunan fungsi sering digunakan untuk menyatakan hubungan antara berbagai variabel dan untuk mengukur sejauh mana suatu besaran fisika berubah terhadap waktu atau variabel lainnya. Beberapa konsep turunan fungsi yang umum digunakan dalam fisika melibatkan kecepatan, percepatan, dan laju perubahan suatu besaran terhadap besaran lainnya. 

Konsep turunan ini memberikan cara matematis untuk menggambarkan perubahan atau laju perubahan dalam berbagai fenomena fisika. Turunan seringkali memainkan peran penting dalam pembentukan persamaan diferensial yang menggambarkan perilaku sistem fisika.

Dalam ekonomi

Turunan fungsi digunakan untuk menyatakan hubungan antara berbagai variabel ekonomi dan untuk mengukur perubahan suatu besaran ekonomi terhadap variabel lainnya. Beberapa contoh penggunaan turunan dalam ekonomi melibatkan konsep elastisitas, produksi, dan utilitas. 

Konsep turunan membantu para ekonom untuk memahami respons sistem ekonomi terhadap perubahan dalam variabel-variabel kunci dan mengukur dampak perubahan tersebut pada keputusan ekonomi. Ini memungkinkan ekonom untuk mengambil keputusan yang lebih informasional dan mendalam dalam menganalisis fenomena ekonomi.

Dalam rekayasa

Turunan fungsi sangat penting karena membantu insinyur untuk memahami dan mengoptimalkan berbagai fenomena fisika atau matematika yang muncul dalam perancangan dan analisis sistem rekayasa. Beberapa aplikasi turunan dalam rekayasa melibatkan analisis sinyal, kontrol sistem, optimisasi, dan permodelan sistem fisik. Berikut adalah beberapa contoh penggunaan turunan dalam rekayasa:

1. Analisis Sinyal (Signal Analysis):
   - Dalam pemrosesan sinyal, turunan sering digunakan untuk menganalisis karakteristik sinyal. Turunan sinyal dapat memberikan informasi tentang frekuensi, amplitudo, dan fase.

2. Kontrol Sistem (Control Systems):
   - Dalam analisis dan desain sistem kontrol, turunan sering digunakan untuk mengukur laju perubahan suatu variabel terhadap waktu. Misalnya, turunan posisi terhadap waktu memberikan kecepatan, dan turunan kecepatan memberikan percepatan.

3. Optimisasi (Optimization):
   - Dalam masalah optimisasi, turunan digunakan untuk menemukan nilai minimum atau maksimum suatu fungsi. Turunan pertama dan kedua sering digunakan dalam analisis titik stasioner (titik kritis) untuk menentukan apakah suatu solusi merupakan minimum, maksimum, atau titik saddle.

4. Permodelan Dinamis Sistem Fisik:
   - Turunan berperan penting dalam permodelan matematis sistem fisik yang dinamis, seperti persamaan gerak dalam mekanika atau hukum-hukum dasar elektronika.

5. Pemrosesan Citra (Image Processing):
   - Dalam pemrosesan citra, turunan dapat digunakan untuk mendeteksi tepi atau perubahan intensitas dalam citra.

6. Analisis Struktur (Structural Analysis):
   - Dalam analisis struktur, turunan digunakan untuk menghitung momen, tegangan, dan deformasi dalam elemen struktural. Turunan juga digunakan dalam permodelan respons dinamis struktur terhadap beban dinamis.

7. Analisis Perpindahan Panas (Heat Transfer Analysis):
   - Dalam analisis perpindahan panas, turunan digunakan untuk menghitung gradien suhu dan menggambarkan distribusi panas dalam suatu sistem.

8. Analisis Sistem Elektromagnetik:
   - Dalam analisis sistem elektromagnetik, turunan digunakan untuk memodelkan hubungan antara medan elektromagnetik dan sirkuit listrik.

Turunan juga terlibat dalam pembuatan model matematis sistem dan memainkan peran penting dalam analisis numerik untuk memecahkan persamaan diferensial dan permasalahan matematika lainnya yang muncul dalam rekayasa. Oleh karena itu, pemahaman yang kuat tentang konsep turunan sangat penting bagi insinyur rekayasa.
Bimbingan Belajar,Ilmu Pengetahuan,
y adalah fungsi dari x atau y=f(x), turunan fungsi dinotasikan sebagai y' atau f ‘(x) atau dy/dx
Maka turunan fungsi y=f(x) terhadap x didefinisikan sebagai :
Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Rumus 1






A. Definisi


Untuk y adalah fungsi dari x atau y=f(x), turunan fungsi dinotasikan sebagai y' atau f ‘(x) atau dy/dx
Maka turunan fungsi y=f(x) terhadap x didefinisikan sebagai :


Contoh :
Jika f (x)=x2 – 3x, maka turunan fungsi f (x)adalah

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Rumus 2


B.      Rumus Dasar Turunan


  1. ·        Turunan fungsi konstan k. Jika f(x)=k, maka  f ‘(x)=0
  2. ·        Jika f(x)=ax, maka f ‘(x)=a
  3. ·        Jika f(x)=axn, maka f ‘(x)=anxn-1
  4. ·        Jika f(x)=u(x) + v(x), maka f ‘(x)=u’(x) + v’(x)
  5. ·        Jika f(x)=u(x) . v(x), maka f ‘(x)=u’(x) .v(x) + v’(x) . u(x)
·       6.               Jika f(x)=u(x) 
                                        v(x)
                   maka f ‘(x)= u’(x) . v(x) + v’(x) . u(x)
                                                   [v(x)]²


·                 7.        Jika f(x)=[u(x)]n, maka f‘(x)=n [u(x)]n-1.u’(x)
·                 8.   Turunan fungsi komposisi (dalil rantai)
              Jika y=f(g(x)), maka  =dy  = dy .dg
                                   dx     dg   dx


TURUNAN FUNGSI TRIGONOMETRI




  • Jika f(x)=sin x, maka f’(x)=cos x
         dan jika f(x)=sin u(x), makaf’(x)=u’(x). cos u(x)

  • Jika f(x)=cos x, maka f’(x)=-sin x
        dan jika f(x)=cos u(x), makaf’(x)=-u’(x). sin u(x)
  •  Jika f(x)=tan x, maka f’(x)=sec2x
PERSAMAAN GARIS SINGGUNG DAN GARIS NORMAL KURVA

  • ·        Gradien garis singgung kurva di titik (x1,y1)pada kurva f(x) adalah m=f’(x1)


Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Gradien


          Persamaan garis singgung kurva
          y – y1=m (x – x1)
·         
  •     Garis normal kurva adalah suatu garis yang tegaklurus dengan garis singgung kurva di titik yang sama dengan titik singgungkurva.

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Kurva

·                    Gradiengaris normal kurva di titik (x1,y1) pada kurva f(x)                          
a           adalah mn=-1/f'(x)  
·                           Persamaan garis normal kurva
        y – y1=mn (x – x1)


FUNGSI NAIK, FUNGSI TURUN DAN NILAI STASIONER


  • ·        Fungsi naik

Suatu fungsi dikatakan naik dalam suatuselang untuk x1 < x2 maka f(x1) < f(x2)
kurva naik jika f’(x) > 0
  • ·        Fungsi turun

Suatu fungsi dikatakan turun dalam suatuselang untuk x1 < x2 maka f(x1) > f(x2)
kurva naik jika f’(x) < 0
  • ·        Nilai dan titik stasioner

Jika fungsi f(x) mempunyai turunan pada x=a dan f’(a)=0, maka f(a) merupakan nilai stasioner fungsi f(x)

Jika f’(a)=0, maka titik stasioner fungsiadalah (a, f(a))
·        Jenis nilai stasioner dimana f”(x) adalahturunan kedua fungsi f(x)

Jika f”(a) < 0, maka f(a) berjenismaksimum

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Kurva 2



Jika f”(a) > 0, maka f(a) berjenis minimum


Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Kurva 3


Jika f”(a)= 0, maka (a, f(a)) adalah titik belok

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990
Kurva 4
  
                                                                          

CONTOH SOAL DAN PEMBAHASAN


    1. Turunan pertama dari fungsi f(x)=4x3 -3x2 + 8x -5 adalah….

          Pembahasan:

        f’(x)  =4.3.x3-1 – 3.2.x2-1+ 8.1 x1-1 -5.0.x0-1
               =12x2 – 6x1 + 8x0 – 0
               =12x2 – 6x + 8
     2.  Turunan pertama dari fungsi y=(3x2+2) (2x -5) adalah…

         Pembahasan:

       misal u(x)=3x2 +2,  u’(x)=6x
       v(x)=2x -5,    v’(x)=2
       maka y’=u’(x) . v(x) + v’(x) . u(x)
                  =6x (2x – 5) + 2 (3x2+2)
                  =12x2 – 30 x + 6 x2+ 4
                  =18x2 – 30x + 4   
                                         
     3. Turunan pertama dari  dari y=(5x2 +3 x)3adalah…

           Pembahasan:

         misal u(x)=(5x2 +3x),  u’(x)=10x + 3
            y=[u(x)]n, 
            maka y' =n [u(x)]n-1.u’(x)
    = 3(5x2 +3x)2(10x + 3)
    =  (30x + 9)(5x2 +3x)2

1.                  4.  Turunan pertama dari fungsi y=∛(6x+5) adalah…

         Pembahasan:

 y=(6x + 5)1/3,u(x)=6x=5, u’(x)=6
 y’=1/3 (6x + 5)-2/3(6)
    =2(6x + 5)-2/3
    =     2       
       ∛(6x+5)²

5. Turunan pertama dari fungsi f(x)=3x + 2 adalah…
                                                    x - 1

                    Pembahasan:

            u(x)=3x+2, u’(x)=3
            v(x)=x-1,    v’(x)=1


     maka f ‘(x)= u’(x) . v(x) - v’(x) . u(x)
                                       [v(x)]²
                                =3(x-1) - 1(3x+2) 
                                           (x-1)²
                                =   -5    
                                     (x-1)²
      6.  Persamaan garis singgung para bola y=x2+ 4x -5 
                 pada titik (-1,2) adalah…

                Pembahasan:

             y’=2x + 4
             m=2(-1) + 4=2
             persamaan garis singgung
             y – 2=2 (x –(-1))
             y – 2=2x + 2
             y=2x + 4

2    7.   Persamaan garis normal kurva y=x3-4x2+ 5x-2 
                 pada titik (2,-5) adalah…

                Pembahasan:

             y’=3x2- 8x + 5=3(2)2– 8(2) + 5=1
             mn=-1/y’=-1/1=-1
             persamaan garis normal
             y – (-5)=-1(x-2)
             y + 5=-x + 2
             y=-x -7

8.   8. Fungsi f(x)=x2 – 9x naik pada interval…

                Pembahasan:

             fungsi naik jika f’(x) > 0 , 
             maka 2x –9 > 0
             jadi fungsi naik pada x > 4,5

9.   9. Tentukan nilai stasioner dari fungsi f(x)=2x3 – 15x2 +36x – 10 !

                 Pembahasan:

              titik stasioner dicapai jika f’(x)=0
              6x2 -30x + 36=0
              6 (x -2) (x-3)=0
              x1=2, x2=3
              Nilai stasioner didapat
              f(2)=18 dan
              f(3)=17

          10. Tentukan turunan pertama dari y=sin³(2x+3)

               Pembahasan :

               y'=3sin²(2x+3).cos(2x+3) (2)
                  =6sin²(2x+3).cos(2x+3)

https://www.radarhot.com/2018/03/turunan-fungsi.html

Continue reading
Subscribe to: Posts (Atom)